Originariamente inviato da MItaly
Come dice Wikipedia, la deviazione standard è normalmente la radice della varianza, ossia è un indice di quanto sono sparpagliati i dati attorno alla media. Se la distribuzione dei tuoi dati è gaussiana (e in genere misure affette da perturbazioni piccole e casuali più o meno lo sono) la deviazione standard ti dice che circa il 68% dei risultati cade entro una deviazione standard di distanza dalla media.
In altre parole, se tu fai un istogramma dei tuoi risultati, facilmente ottieni una curva gaussiana del tipo:

la media ti dice dove sta il centro della tua gaussiana, la deviazione standard quanto è larga.
Per cui, sui tempi di elaborazione:
- una media bassa ovviamente è preferibile (compatibilmente con l'accuratezza del risultato, naturalmente)
- una deviazione standard bassa ti indica che più o meno ci mette sempre quel tempo lì; una deviazione standard alta, invece, indica che c'è grande variabilità sul tempo di elaborazione, per cui se ti serve avere una funzione con tempistiche molto consistenti (se, ad esempio, hai delle deadline temporali o altri problemi del genere) potresti dover cercare altrove.
Per quanto riguarda i valori di accuratezza, dipende da come li misuri: se misuri semplicemente la discrepanza (non in valore assoluto), ovvero la differenza tra valore ottenuto e valore vero:
- la media della discrepanza deve essere il più possibile vicina allo zero; se non lo è e la deviazione standard è piccola può essere indice di un errore sistematico
- e se anche la media è perfettamente zero, qui il punto chiave è la deviazione standard: potresti avere una funzione che restituisce valori estremamente sballati verso l'alto e verso il basso, ma questi nella media si compensano; la deviazione standard, invece, ti indica lo sparpagliamento attorno alla media, per cui se è alta capisci subito che c'è il comportamento della funzione non è consistente.
Se invece prendi la discrepanza in valore assoluto (o, anche meglio, al quadrato, in modo da far pesare di più discrepanze grosse), già dalla media hai un'indicazione sicura del fatto che la tua funzione sgarri sistematicamente, dato che, avendo a che fare con soli valori positivi, non è possibile avere compensazioni sulla media; la deviazione standard qui ti dice invece se lo "sgarro" è più o meno sempre costante (errore sistematico) o variabile.
Una cosa interessante per vedere a colpo eventuali correlazioni può essere fare uno scatter plot, mettendo ad esempio sulle ascisse il tempo di esecuzione e sulle ordinate la discrepanza dal valore vero; in questo modo puoi vedere subito se c'è una qualche correlazione tra la velocità dell'algoritmo e la sua imprecisione. Ovviamente con altre scelte di grandezze da mettere nel grafico puoi cercare altre correlazioni.


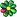


 Rispondi quotando
Rispondi quotando